LogoCSP Wiki By Yundou
3 DS

Splay 树

本页面将简要介绍如何用 Splay 维护二叉查找树。

定义

Splay 树，或 伸展树，是一种平衡二叉查找树，它通过 伸展（splay）操作 不断将某个节点旋转到根节点，使得整棵树仍然满足二叉查找树的性质，能够在均摊 O(log⁡N)O(\log N) 时间内完成插入、查找和删除操作，并且保持平衡而不至于退化为链。

Splay 树由 Daniel Sleator 和 Robert Tarjan 于 1985 年发明。

基本结构与操作

本节讨论 Splay 树的基本结构和它的核心操作，其中最为重要的是伸展操作。

Splay 树是一棵二叉查找树，查找某个值时满足性质：左子树任意节点的值 << 根节点的值 << 右子树任意节点的值。

维护信息

本文使用数组模拟指针来实现 Splay 树，需要维护如下信息：

rtidfa[i]ch[i][0/1]val[i]cnt[i]sz[i]
根节点编号已使用节点个数父亲左右儿子编号节点权值权值出现次数子树大小

初始化时，所有信息都置零即可。

辅助操作

首先是一些简单的辅助操作：

  • dir(x)：判断节点 xx 是父亲节点的左儿子还是右儿子；
  • push_up(x)：在改变节点位置后，根据子节点信息更新节点 xx 的信息。
bool dir(int x) { return x == ch[fa[x]][1]; }

void push_up(int x) { sz[x] = cnt[x] + sz[ch[x][0]] + sz[ch[x][1]]; }

旋转操作

为了使 Splay 保持平衡，需要进行旋转操作。旋转的作用是将某个节点上移一个位置。

旋转需要保证：

  • 整棵 Splay 的中序遍历不变（不能破坏二叉查找树的性质）；
  • 受影响的节点维护的信息依然正确有效；
  • rt 必须指向旋转后的根节点。

在 Splay 中旋转分为两种：左旋和右旋。

图片描述

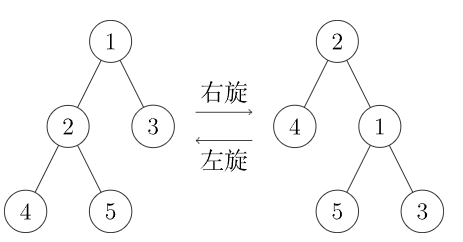
观察图示可知，如果要通过旋转将节点 xx（左旋时的 11 和右旋时的 22）上移，则旋转的方向由该节点是其父节点的左节点还是右节点唯一确定。因此，实现旋转操作时，只需要将要上移的节点 xx 传入即可。

具体分析旋转步骤：（假设需要上移的节点为 xx，以右旋为例）

  1. 首先，记录节点 xx 的父节点 yy，以及 yy 的父节点 zz（可能为空），并记录 xx 是 yy 的左子节点还是右子节点；
  2. 按照旋转后的树中自下向上的顺序，依次更新 yy 的左子节点为 xx 的右子节点，xx 的右子节点为 yy，以及若 zz 非空，zz 的子节点为 xx；
  3. 按照同样的顺序，依次更新当前 yy 的左子节点（若存在）的父节点为 yy，yy 的父节点为 xx，以及 xx 的父节点为 zz；
  4. 自下而上维护节点信息。
void rotate(int x) {
  int y = fa[x], z = fa[y];
  bool r = dir(x);
  ch[y][r] = ch[x][!r];
  ch[x][!r] = y;
  if (z) ch[z][dir(y)] = x;
  if (ch[y][r]) fa[ch[y][r]] = y;
  fa[y] = x;
  fa[x] = z;
  push_up(y);
  push_up(x);
}

在所有函数的实现时，都应注意不要修改节点 00 的信息。

伸展操作

Splay 树要求每访问一个节点 xx 后都要强制将其旋转到根节点。该操作也称为伸展操作。

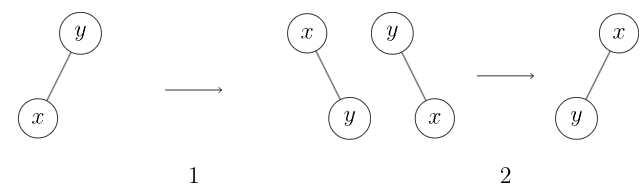
设刚访问的节点为 xx。要做伸展操作，就是要对 xx 做一系列的 伸展步骤。每次对 xx 做一次伸展步骤，xx 到根节点的距离都会更近。定义 pp 为 xx 的父节点。伸展步骤有三种：

  1. zig: 在 pp 是根节点时操作。Splay 树会根据 xx 和 pp 间的边旋转。zig 存在是用于处理奇偶校验问题，仅当 xx 在伸展操作开始时具有奇数深度时作为伸展操作的最后一步执行。
图片描述

即直接将 xx 右旋或左旋（图 1, 2）。

图片描述
  1. zig-zig: 在 pp 不是根节点且 xx 和 pp 都是右侧子节点或都是左侧子节点时操作。下方例图显示了 xx 和 pp 都是左侧子节点时的情况。Splay 树首先按照连接 pp 与其父节点 gg 边旋转，然后按照连接 xx 和 pp 的边旋转。
图片描述

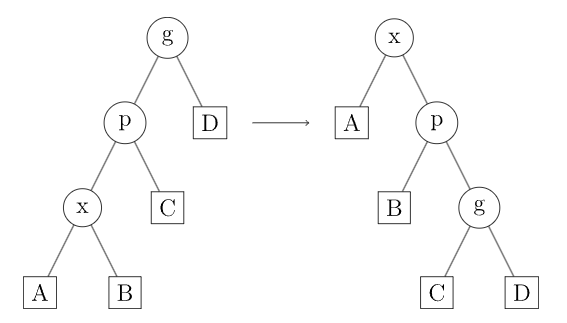
即首先将 pp 右旋或左旋，然后将 xx 右旋或左旋（图 3, 4）。

图片描述
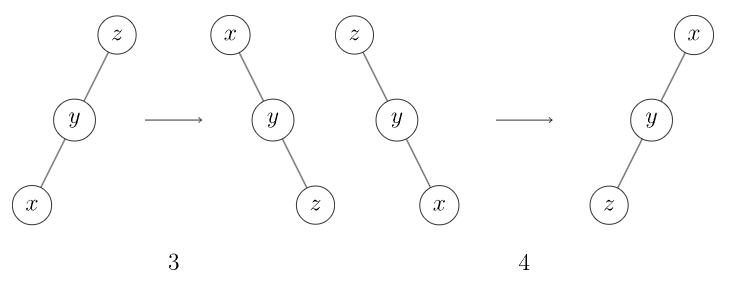
  1. zig-zag: 在 pp 不是根节点且 xx 和 pp 一个是右侧子节点一个是左侧子节点时操作。Splay 树首先按 pp 和 xx 之间的边旋转，然后按 xx 和 gg 新生成的结果边旋转。
图片描述

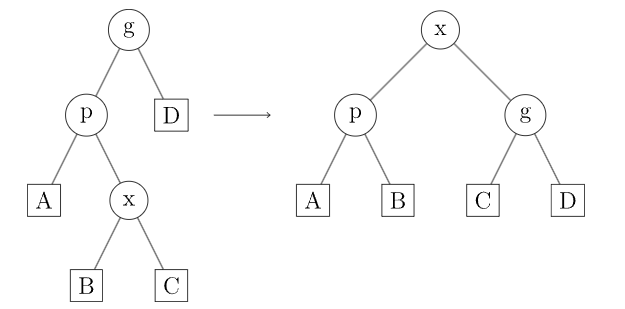
即将 xx 先左旋再右旋或先右旋再左旋（图 5, 6）。

图片描述

请读者尝试自行模拟 66 种旋转情况，以理解伸展操作的基本思想。

比较三种伸展步骤可知，要区分此时应使用哪种操作，关键是要判断 xx 是否是根节点的子节点，以及 xx 和它父节点是否在各自的父节点同侧。

此处提供的实现，可以指定任意根节点 zz，并将它的子树内任意节点 xx 上移至 zz 处：

  1. 首先记录根节点 zz 的父节点 ww，从而可以利用 fa[x] == w 判断 xx 已经位于根结点处；
  2. 记录 xx 当前的父节点 yy，如果 yy 和 ww 相同，说明 xx 已经到达根节点；
  3. 否则，利用 fa[y] == w 判断 yy 是否是根节点。如果是，直接做 zig 操作将 xx 旋转；如果不是，利用 dir(x) == dir(y) 判断使用 zig-zig 还是 zig-zag，前者先旋转 yy 再旋转 xx，后者直接旋转两次 xx。
void splay(int& z, int x) {
  int w = fa[z];
  for (int y; (y = fa[x]) != w; rotate(x)) {
    if (fa[y] != w) rotate(dir(x) == dir(y) ? y : x);
  }
  z = x;
}

伸展操作是 Splay 树的核心操作，也是它的时间复杂度能够得到保证的关键步骤。请务必保证每次向下访问节点后，都进行一次伸展操作。

另外，伸展操作会将当前节点 xx 到根节点 zz 的路径上的所有节点信息自下而上地更新一遍。正是因为这一点，才可以修改非根节点，再通过伸展操作将它上移至根来完成整个树的信息更新。

时间复杂度

对大小为 nn 的 Splay 树做 mm 次伸展操作的复杂度是 O((n+m)log⁡n)O((n+m)\log n) 的，单次均摊复杂度是 O(log⁡n)O(\log n) 的。

平衡树操作

本节讨论基于 Splay 树实现平衡树的常见操作的方法。其中，较为重要的是按照值或排名查找元素，它们可以将某个特定的元素找到，并上移至根节点处，以便后续处理。

作为例子，本节将讨论模板题目普通平衡树的实现。

按照值查找

作为二叉查找树，可以通过值 vv 查找到相应的节点，只需要将待查找的值 vv 和当前节点的值比较即可，找到后将该元素上移至根部即可。

应注意，经常存在树中不存在相应的节点的情形。对于这种情形，要记录最后一个访问的节点（即实现中的 yy），并将 yy 上移至根部。此时，节点 yy 存储的值必然要么是所有小于 vv 的元素中最大的（即 vv 的前驱），要么是所有大于 vv 的元素中最小的（即 vv 的后继）。这是因为查找过程保证，左子树总是存储小于 vv 的值，而右子树总是存储大于 vv 的值。

void find(int& z, int v) {
  int x = z, y = fa[x];
  for (; x && val[x] != v; x = ch[y = x][v > val[x]]);
  splay(z, x ? x : y);
}

该实现允许指定任何节点 zz 作为根节点，并在它的子树内按值查找。

按照排名访问

因为记录了子树大小信息，所以 Splay 树还可以通过排名访问元素，即查找树中第 kk 小的元素。

设 kk 为剩余排名，具体步骤如下：

  • 如果左子树非空且剩余排名 kk 不大于左子树的大小，那么向左子树查找；
  • 否则，如果 kk 不大于左子树加上根的大小，那么根节点就是要寻找的；
  • 否则，将 kk 减去左子树的和根的大小，继续向右子树查找；
  • 将最终找到的元素上移至根部。
void loc(int& z, int k) {
  int x = z;
  for (;;) {
    if (sz[ch[x][0]] >= k) {
      x = ch[x][0];
    } else if (sz[ch[x][0]] + cnt[x] >= k) {
      break;
    } else {
      k -= sz[ch[x][0]] + cnt[x];
      x = ch[x][1];
    }
  }
  splay(z, x);
}

该实现需要保证排名 kk 不超过根 zz 处的树大小。

模板题目中操作 44 要求按照排名返回值，直接调用该方法，并返回值即可。

int find_kth(int k) {
  if (k > sz[rt]) return -1;
  loc(rt, k);
  return val[rt];
}

合并操作

有些时候需要合并两棵 Splay 树。

设两棵树的根节点分别为 xx 和 yy，那么为了保证结果仍是二叉查找树，需要要求 xx 树中的最大值小于 yy 树中的最小值。这条件通常都可以满足，因为两棵树往往是从更大的子树中分裂出的。

合并操作如下：

  • 如果 xx 和 yy 其中之一或两者都为空树，直接返回不为空的那一棵树的根节点或空树；
  • 否则，通过 loc(y, 1) 将 yy 树中的最小值上移至根 yy 处，再将它的左节点（此时必然为空）设置为 xx，并更新节点信息，返回节点 yy。
int merge(int x, int y) {
  if (!x || !y) return x | y;
  loc(y, 1);
  ch[y][0] = x;
  fa[x] = y;
  push_up(y);
  return y;
}

分裂操作类似。因而，Splay 树可以模拟 无旋 treap 的思路做各种操作，包括区间操作。后文 会介绍更具有 Splay 树风格的区间操作处理方法。

插入操作

插入操作是一个比较复杂的过程。具体步骤如下：（假设插入的值为 vv）

  • 类似按值查找的过程，根据 vv 向下查找到存储 vv 的节点或者空节点，过程中记录父节点 yy；
  • 如果存在存储 vv 的节点 xx，直接更新信息，否则就新建节点 xx；
  • 做伸展操作，将最后一个节点 xx 上移至根部。
void insert(int v) {
  int x = rt, y = 0;
  for (; x && val[x] != v; x = ch[y = x][v > val[x]]);
  if (x) {
    ++cnt[x];
    ++sz[x];
  } else {
    x = ++id;
    val[x] = v;
    cnt[x] = sz[x] = 1;
    fa[x] = y;
    if (y) ch[y][v > val[y]] = x;
  }
  splay(rt, x);
}

该实现允许直接向空树内插入值。若不想处理空树，可以在树中提前插入哑节点。

删除操作

删除操作也是一个比较复杂的操作。具体步骤如下：（假设删除的值为 vv）

  • 首先按照值 vv 查找存储它的节点，并上移至根部；
  • 如果不存在存储它的节点，直接返回；（上一步已经做了伸展操作）
  • 否则，更新节点信息；
  • 如果得到的根节点为空节点，就合并左右子树作为新的根节点，注意合并前需要更新两个子树的根的父节点为空。
bool remove(int v) {
  find(rt, v);
  if (!rt || val[rt] != v) return false;
  --cnt[rt];
  --sz[rt];
  if (!cnt[rt]) {
    int x = ch[rt][0];
    int y = ch[rt][1];
    fa[x] = fa[y] = 0;
    rt = merge(x, y);
  }
  return true;
}

查询排名

直接按照值 vv 访问节点（并上移至根），然后返回相应的值即可。

注意，当 vv 不存在时，方法 find(rt, v) 返回的根和 vv 的大小关系无法确定，需要单独讨论。

int find_rank(int v) {
  find(rt, v);
  return sz[ch[rt][0]] + (val[rt] < v ? cnt[rt] : 0) + 1;
}

查询前驱

前驱定义为小于 vv 的最大的数。具体步骤如下：

  • 按照值 vv 访问节点（并上移至根部）；
  • 如果根部的值小于 vv，那么它必然是最大的那个，直接返回；
  • 否则，在左子树中找到最大值，并上移至根部。

最后一步相当于直接调用 loc(ch[rt][0], cnt[ch[rt][0]])，只是省去了不必要的判断。

int find_prev(int v) {
  find(rt, v);
  if (rt && val[rt] < v) return val[rt];
  int x = ch[rt][0];
  if (!x) return -1;
  for (; ch[x][1]; x = ch[x][1]);
  splay(rt, x);
  return val[rt];
}

该实现允许前驱不存在，此时返回 −1-1。

查询后继

后继定义为大于 xx 的最小的数。查询方法和前驱类似，只是将左子树的最大值换成了右子树的最小值，即调用 loc(ch[rt][1], 1)。

int find_next(int v) {
  find(rt, v);
  if (rt && val[rt] > v) return val[rt];
  int x = ch[rt][1];
  if (!x) return -1;
  for (; ch[x][0]; x = ch[x][0]);
  splay(rt, x);
  return val[rt];
}

参考实现

本节的最后，给出模板的参考实现。

#include <iostream>

constexpr int N = 2e6;
int id, rt;
int fa[N], val[N], cnt[N], sz[N], ch[N][2];

bool dir(int x) { return x == ch[fa[x]][1]; }

void push_up(int x) { sz[x] = cnt[x] + sz[ch[x][0]] + sz[ch[x][1]]; }

void rotate(int x) {
  int y = fa[x], z = fa[y];
  bool r = dir(x);
  ch[y][r] = ch[x][!r];
  ch[x][!r] = y;
  if (z) ch[z][dir(y)] = x;
  if (ch[y][r]) fa[ch[y][r]] = y;
  fa[y] = x;
  fa[x] = z;
  push_up(y);
  push_up(x);
}

void splay(int& z, int x) {
  int w = fa[z];
  for (int y; (y = fa[x]) != w; rotate(x)) {
    if (fa[y] != w) rotate(dir(x) == dir(y) ? y : x);
  }
  z = x;
}

void find(int& z, int v) {
  int x = z, y = fa[x];
  for (; x && val[x] != v; x = ch[y = x][v > val[x]]);
  splay(z, x ? x : y);
}

void loc(int& z, int k) {
  int x = z;
  for (;;) {
    if (sz[ch[x][0]] >= k) {
      x = ch[x][0];
    } else if (sz[ch[x][0]] + cnt[x] >= k) {
      break;
    } else {
      k -= sz[ch[x][0]] + cnt[x];
      x = ch[x][1];
    }
  }
  splay(z, x);
}

int merge(int x, int y) {
  if (!x || !y) return x | y;
  loc(y, 1);
  ch[y][0] = x;
  fa[x] = y;
  push_up(y);
  return y;
}

void insert(int v) {
  int x = rt, y = 0;
  for (; x && val[x] != v; x = ch[y = x][v > val[x]]);
  if (x) {
    ++cnt[x];
    ++sz[x];
  } else {
    x = ++id;
    val[x] = v;
    cnt[x] = sz[x] = 1;
    fa[x] = y;
    if (y) ch[y][v > val[y]] = x;
  }
  splay(rt, x);
}

bool remove(int v) {
  find(rt, v);
  if (!rt || val[rt] != v) return false;
  --cnt[rt];
  --sz[rt];
  if (!cnt[rt]) {
    int x = ch[rt][0];
    int y = ch[rt][1];
    fa[x] = fa[y] = 0;
    rt = merge(x, y);
  }
  return true;
}

int find_rank(int v) {
  find(rt, v);
  return sz[ch[rt][0]] + (val[rt] < v ? cnt[rt] : 0) + 1;
}

int find_kth(int k) {
  if (k > sz[rt]) return -1;
  loc(rt, k);
  return val[rt];
}

int find_prev(int v) {
  find(rt, v);
  if (rt && val[rt] < v) return val[rt];
  int x = ch[rt][0];
  if (!x) return -1;
  for (; ch[x][1]; x = ch[x][1]);
  splay(rt, x);
  return val[rt];
}

int find_next(int v) {
  find(rt, v);
  if (rt && val[rt] > v) return val[rt];
  int x = ch[rt][1];
  if (!x) return -1;
  for (; ch[x][0]; x = ch[x][0]);
  splay(rt, x);
  return val[rt];
}

int main() {
  int n;
  std::cin >> n;
  for (; n; --n) {
    int op, x;
    std::cin >> op >> x;
    switch (op) {
      case 1:
        insert(x);
        break;
      case 2:
        remove(x);
        break;
      case 3:
        std::cout << find_rank(x) << '\n';
        break;
      case 4:
        std::cout << find_kth(x) << '\n';
        break;
      case 5:
        std::cout << find_prev(x) << '\n';
        break;
      case 6:
        std::cout << find_next(x) << '\n';
        break;
    }
  }
  return 0;
}

例题：

Status
Problem
Tags
P3369. 【模板】普通平衡树
数据结构
P1486. 郁闷的出纳员
数据结构

二叉搜索树与平衡树

Previous Page

Treap

Next Page